Geometría 1) Dados los puntos A(1, 3, 2) y B(0, 1, 2):
a) Halla
m y
n para que los puntos A, B y C(2,
m,
n) estén alineados.
b) Halla el simétrico del punto B respecto al punto A.
Solución2) Dado el punto P(2, –1, 3), halla las ecuaciones de los siguientes planos:
a) Paralelo a 2x + 3y – z + 4 = 0 y que contiene a P.
b) Perpendicular a la recta

y que contiene a P.
Solución3) Estudia la posición relativa del plano
p: 2x – y + 3z = 8 y la recta
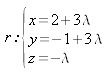 Solución
Solución4) Un tetraedro tiene por vértices A(2, 1, 0), B(3, 4, 0) y C(5, 1, 0). El cuarto vértice, D, está sobre la recta

.
Halla las coordenadas de D para que el volumen del tetraedro sea 6 unidades cúbicas.
Solución5) Halla el punto de

cuya distancia al punto P(1, 0, 2) sea
 Solución
Solución6) Sea la recta

y el plano
p: 2x – 3y + z + 1 = 0:
a) Calcula el seno del ángulo que forman r y
p.
b) Calcula P', proyección del punto P(1, 0, 0) en el plano
p.
c) Halla la distancia del punto P(1, 0, 0) al plano
p.
d) Halla el punto Q, intersección de r y
p.
e) Halla la ecuación continua de la recta que pasa por P' y Q.
SoluciónNota: El ejercicio 6 vale 2'5 puntos, el resto 1'5 cada uno.
Pronto pondré las soluciones.





 y que contiene a P.
y que contiene a P.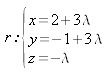
 .
. cuya distancia al punto P(1, 0, 2) sea
cuya distancia al punto P(1, 0, 2) sea 
 y el plano p: 2x – 3y + z + 1 = 0:
y el plano p: 2x – 3y + z + 1 = 0: