1ª Evaluación
1) Se considera el sistema de ecuaciones lineales:
a) Encuentra un valor de a para el cual el sistema sea incompatible.
b) Discute si existe algún valor del parámetro a para el cual el sistema sea compatible determinado.
c) Resuelve el sistema para a = 0.
Solución
2) Halla, en función de a, el rango de la matriz
y calcula, si existe, la matriz inversa A-1 en los casos a = 1 y a = –1.Solución
2ª Evaluación
3) Halla el punto simétrico de P(1, 0, 3) respecto del plano
p: x – 3y – 2z + 4 = 0
Solución
4) Dadas la recta r, determinada por los puntos A(1, 1, 1) y B(3, 1, 2), y la recta
estudia su posición relativa y halla, si existe, la ecuación del plano que las contiene.Solución
3ª Evaluación
5) Calcula m y n para que la siguiente función sea continua y derivable en R:
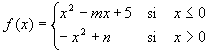
Solución
6) Calcula la derivada de:
a) y = sen x cos x. Solución
b)
Solución7) De la función f(x) = ax3 + bx sabemos que pasa por (1, 1) y en ese punto tiene tangente paralela a la recta 3x + y = 0.
a) Halla a y b.
b) Determina sus extremos relativos y sus intervalos de crecimiento y decrecimiento.
Solución
8) Calcula las integrales:
a)
b)
Solución
, definida para x > 0:
