Examen 2a Evaluación (2)

jb
Otra oportunidad

1)	Dados los vectores u = (a, 1 + a, 2a), v = (a, 1, a) y w = (1, a, 1), se pide: a) Halla los valores de a para los que los vectores u, v y w son linealmente independientes. b) Estudia si el vector a = (3, 3, 0) depende linealmente de u, v y w para el caso a = 2. c) Justifica razonadamente si para a = 0 se cumple la igualdad u·(v×w) = 0 Solución
2)	Halla la ecuación del plano que contiene a la recta y es perpendicular al plano π: 2x + y + z – 2 = 0. Calcula el ángulo que forman la recta r y el plano π Solución
3)	Dadas las rectas: calcula a y b para que sean ortogonales y coplanarias. Solución
4)	Dados el punto P(2, 0, –3), la recta 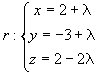y el plano π: x + 2y + 2z – 1 = 0, calcula la distancia entre: a) P y π. b) P y r. Solución
5)	Calcula los límites: a) b) Solución

jb