| 1) | Dados los vectores u = (2, –1, 1), v = (3, 1, –2) y w = (4, –1, 5): a) Halla un vector, de módulo 1, que sea perpendicular a u y a v. b) Halla el volumen del paralelepípedo determinado por u, v y w. Solución |
| 2) | Considera los planos π ≡ 2x + ay + 4z – 1 = 0 y σ ≡ ax + 2y + 4z – 3 = 0 a) Calcula el ángulo que forman π y σ cuando a = 1. b) Halla a para que π y σ sean paralelos. c) Determina el valor de a para que π y σ sean perpendiculares. Solución |
| 3) | Estudia la posición relativa de estas rectas: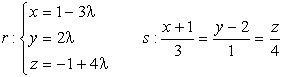 Solución |
| 4) | Obtén el punto simétrico de P(-2, 1, 5) respecto a la recta Solución |
| 5) | a) Calcula el límite: Solución b) Dada la función f(x) = x5 + 2x + 1, encuentra un intervalo de amplitud menor que 2 en el que f(x) corta al eje OX. Solución |
jb
No hay comentarios:
Publicar un comentario