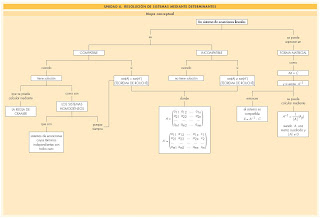
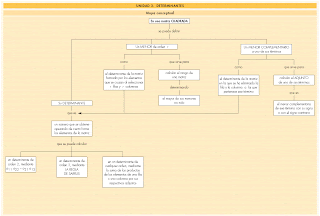
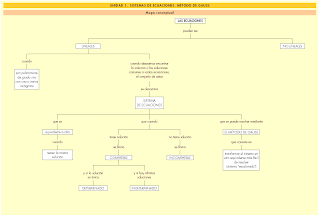
Un vistazo global a la unidad: mapa conceptual

Para consultar ejercicios sobre vectores, podéis ir a lo publicado el año pasado:
¤ Tema 5 Vectores
¤ Vectores (II)
¤ Examen Tema 5
También tenéis las soluciones a los ejercicios
jb
"Me lo contaron y lo olvidé. Lo vi y lo entendí. Lo hice y lo aprendí."
Confucio (551-479 a. C.)


 tales que
tales que 
 , calcula el valor de los siguientes determinantes:
, calcula el valor de los siguientes determinantes: b)
b) 


 satisface la igualdad
satisface la igualdad 


 y calcula, si existe, la matriz inversa A-1 en los casos a = 1 y a = –1.
y calcula, si existe, la matriz inversa A-1 en los casos a = 1 y a = –1. estudia su posición relativa y halla, si existe, la ecuación del plano que las contiene.
estudia su posición relativa y halla, si existe, la ecuación del plano que las contiene.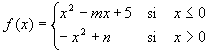
 Solución
Solución


 Solución
Solución , definida para x > 0:
, definida para x > 0: Solución
Solución Solución
Solución
















