Examen septiembre

jb
El examen de septiembre será el

Viernes 2 de septiembre a las 8:00 horas

Suerte a todos

Podéis consultar el calendario de exámenes de septiembre del
IES Santa Maria d'Eivissa
jb

Examen final, soluciones

jb

Matemáticas II

1)	Si la altura de Luis aumentase el triple de la diferencia entre la altura de Eusebio y de Pablo, Luis sería igual de alto que Pablo. Las alturas de los tres suman 515 cm. Ocho veces la altura de Eusebio es lo mismo que nueve veces la de Luis. Halla las tres alturas. Solución
2)	Desarrolla el siguiente determinante: Solución
3)	Calcula el valor de a para que las rectas: se corten en un punto, y halla el punto de corte. Solución
4)	Dados el punto P(1, 0, –3), la recta , y el plano π: 2x – 3y + z = 0, calcula: a) El valor de m para que r sea paralela a π. b) La distancia de P a π. Solución
5)	Calcula estos límites: a) b) Solución
6)	Deriva las siguientes funciones: a) f(x) = e3x – 2 · cos (4x2 – 3) b) x3 – 3y2 + x2y – 2 = 0. Solución
7)	Resuelve las integrales: a) b) Solución

Nota: Haz un examen limpio, sin borrones. No utilizar lápiz (salvo gráficos).
jb

Examen final

jb
Os recuerdo que el examen final será el

Martes 24 de mayo a las 16:00 horas

Suerte a todos
jb

Examen 3a evaluación, soluciones

jb

3ª evaluación

1)	Calcula a y b para que la siguiente función sea derivable en todo R: Solución
2)	Halla la ecuación de la recta tangente a la curva Solución
3)	Queremos construir una piscina de fondo cuadrado con 32 m3 de capacidad, de modo que la superficie total (las paredes más el fondo) sea mínima. ¿Qué dimensiones ha de tener la piscina? Solución
4)	Resuelve las integrales siguientes: a) b) Solución
5)	Halla el área limitada entre la curva y = x3 – 2x2 – 3x y el eje X. Solución

jb

Examen 3a Evaluación

jb
Os recuerdo que el examen de la tercera evaluación será el

Martes 17 de mayo a las 16:00 horas

Suerte a todos
jb

Tema 13: Integral definida

jb
Mapa conceptual de la unidad:



Para consultar ejercicios sobre integrales, podéis ir a lo publicado anteriormente:

¤ Tema 13 La integral definida
¤ Integral definida
¤ Integral definida (II)
¤ Examen 3a Evaluación
¤ Examen Integrales

Podéis consultar las soluciones a todos los ejercicios del libro.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema.
jb

Tema 12: Cálculo de primitivas

jb
El proceso de integración podemos decir que es el inverso a la derivación, por lo tanto, conviene saberse bien las derivadas para estudiar más fácilmente las integrales.

Veamos el mapa conceptual de la unidad:



Para consultar ejercicios sobre integrales, podéis ir a lo publicado anteriormente:

¤ Integrales
¤ Integrales (II)
¤ Integrales (III)
¤ Integrales (IV)
¤ Integrales (V)

Podéis consultar las soluciones (pdf, 255 kb) a todos los ejercicios del libro.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema.
jb

Examen temas 9, 10 y 11, soluciones

jb

Derivadas

1)	Estudia la derivabilidad de esta función, según los valores de a y b: Solución
2)	Calcula la derivada: a) b) f(x) = (2x + 1)x c) x2+ 3xy + y2 = 0 Solución
3)	Comprueba que la función: 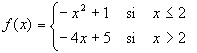satisface las hipótesis del teorema del valor medio en el intervalo [0, 3]. ¿Dónde cumple la tesis? Solución
4)	Un espejo plano tenía forma de un cuadrado de 80 cm de lado y se ha roto por una esquina según una recta. Uno de los trozos tiene forma de triángulo rectángulo de catetos 40 y 32 cm. Halla las dimensiones del espejo rectangular de área máxima que se puede recortar del otro trozo, de modo que los bordes del nuevo espejo sean paralelos a los del primitivo. Solución
5)	Estudia (dominio, crecimiento, asíntotas,... ) y representa esta función: Solución

jb

Pruebas de acceso a la UIB

jb
Han cambiado la página web de la UIB, y el acceso a los exámenes de las PAU de años anteriores ahora es:

http://estudis.uib.es/grau/acces/batxiller/Info_materies/

También están las fechas de las pruebas:
7, 8, y 9 de junio,
13, 14 y 15 de septiembre.

Espero que os sirva de ayuda.

jb

Tema 11: Representación de funciones

jb
En este tema hay que repasar muchos conceptos de años anteriores:
Es conveniente que repaséis el tema de funciones o límites de 1º de Bachillerato

Mapa conceptual de la unidad:



Para consultar ejercicios sobre representación de funciones, podéis ir a lo publicado años anteriores:

¤ Tema 11 Representación de funciones
¤ Dominio, simetrías y periodicidad
¤ Ramas infinitas
¤ Puntos singulares
¤ Representación de funciones (I)
¤ Representación de funciones (II)
¤ Representación de funciones (III)
¤ Representación de funciones (IV)
¤ Soluciones tema 11

También tenéis las soluciones a los ejercicios.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema.
jb

Problemas de optimización

jb
Aquí tenéis resueltos algunos problemas del libro:

1)	Las manecillas de un reloj miden 4 cm y 6 cm, y uniendo sus extremos se forma un triángulo. Determina el instante entre las 12 h y las 12 h 30 min en el que el área del triángulo es máxima.
2)	En una circunferencia de radio r se traza la tangente en un punto cualquiera C y una cuerda AB paralela a dicha tangente. Obtenemos, así, un triángulo ABC cuya área queremos que sea la mayor posible. Demuestra que, para ello, la distancia de C a la cuerda debe ser 3/2 del radio.
3)	En una semicircunferencia de diámetro AB = 2r se traza una cuerda CD paralela a AB. ¿Cuál debe ser la longitud de esa cuerda para que el área del trapecio ABDC sea máxima?
4)	En la figura del problema anterior, llamamos E al punto medio del arco CD y dibujamos el pentágono ACEDB a) Calcula la longitud de la cuerda CD para que el área del pentágono sea máxima. b) Calcula, también, el valor del área máxima del pentágono

jb

¿L'Hôpital o L'Hospital?

jb
¿Cuál es la forma correcta de escribirlo: L'Hôpital o L'Hospital?

En la Wikipedia tenemos una explicación sobre por qué vemos escrito el nombre de las dos maneras, además de un resumen de su relación con Johan Bernoulli.

Breve e interesente.

Citando a un aragonés ilustre:
"Lo bueno, si breve, dos veces bueno, y aún lo malo, si breve, no tan malo."

Baltasar Gracián (1601 – 1658).

jb

Tema 10: Aplicaciones de la derivada

jb
Para empezar el tema: planteamiento didáctico

Programación

Ejercicios con Derive

Criterios de evaluación

Un vistazo global a la unidad: mapa conceptual



Para consultar ejercicios sobre límites, podéis ir a lo publicado años anteriores:

	¤	Tema 10 Aplicaciones de la derivada.
	¤	Aplicaciones de la derivada (II)
	¤	Aplicaciones de la derivada (III) Optimización
	¤	Regla de L'Hôpital-Bernoulli.
	¤	Teorema de Rolle y del valor medio.
	¤	Aplicaciones (VI) Soluciones y cuestiones teóricas.
	¤	Examen temas 9 y 10

Ejercicios sobre Funciones, continuidad y derivabilidad, de la selectividad de la Universidad Illes Balears (desde el año 2001 hasta 2008)

Funciones 1
Funciones 2
Funciones 3
Funciones 4

Los enunciados de los exámenes aquí

Los archivos se abren con Internet Explorer (no funciona con Mozilla) y si sale un aviso:


hay que permitir ejecutar los scripts (Permitir contenido bloqueado...)

También tenéis las soluciones a los ejercicios del libro.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema.

Un capítulo interesante de la Historia de las Matemáticas:
«La Controversia L'Hôpital - Bernoulli».

jb

Curso Derive

jb
Para estudiar estos temas podemos ayudarnos del programa Derive.

Puedes descargarte la versión 6.

Para conocer el programa puedes visitar este curso.
jb

Tema 9: Derivadas

jb
Para empezar el tema: planteamiento didáctico

Programación

Ejercicios con Derive

Criterios de evaluación

Un vistazo global a la unidad: mapa conceptual



Conviene repasar el tema de derivadas de 1º bachillerato

Para consultar ejercicios sobre derivadas, podéis ir a lo publicado otros años:

¤ Tema 9 Derivadas
¤ Derivadas (II)
¤ Derivadas (III)
¤ Derivadas (IV)

En YouTube encontraréis muchos videos de resolución de derivadas, por ejemplo:



También tenéis las soluciones a los ejercicios.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema.
jb

Ex 2a Evaluación Soluciones

jb

Segunda Evaluación

1)	Dados los vectores a = (3, 2, –1) y b = (m, 3, m): a) Halla el valor de m para que a y b sean perpendiculares. b) Para m = 1, halla el área del paralelogramo determinado   por a y b. Solución
2)	Considera los planos π ≡ 2x + ay + 4z – 1 = 0 y σ ≡ ax + 2y + 4z – 3 = 0 a) Calcula el ángulo que forman π y σ cuando a = 1. b) Halla a para que π y σ sean paralelos. c) Determina el valor de a para que π y σ sean perpendiculares. Solución
3)	Halla la ecuación del plano que contiene a la recta y es perpendicular al plano π ≡ 2x + y + z – 2 = 0. Calcula el ángulo que forman la recta r y el plano π. Solución
4)	Obtén el punto simétrico de P(–2, 1, 5) respecto a la recta   ¿Cuál es la distancia entre P y s? Solución
5)	Dada la función f(x) = x5 + x + 1, encuentra un intervalo de amplitud menor que 2 en el que f(x) corta al eje OX. Solución
6)	La altura media (en metros) de una determinada especie de pinos viene dada por la función   a) Hallar k para que sea una función continua. b) Representa la función para un período de 15 años. c) ¿A cuánto tiende la altura media de estos árboles   con el paso del tiempo? Solución

jb

Examen temas 7 y 8 Soluciones

jb

Temas 7 y 8

1)	Halla el lugar geométrico de los puntos que equidistan de los planos de ecuaciones 3x – 4y + 5 = 0 y 2x – 2y + z + 9 = 0 Solución
2)	Los puntos P(0, 1, 0) y Q(–1, 1, 1) son dos vértices de un triángulo, y el tercero, S, pertenece a la recta . La recta que contiene a P y a S es perpendicular a la recta r. a) Determina las coordenadas de S. b) Calcula el área del triángulo PQS Solución
3)	Calcula: y Solución
4)	¿Tiene alguna raíz real la ecuación sen x + 2x + 1 = 0? Justifícalo. Si la respuesta es afirmativa, determina un intervalo de amplitud menor que 2 en el que se encuentre la raíz. Solución
5)	En una empresa se hacen montajes en cadena. El número de montajes realizados por un trabajador sin experiencia depende de los días de entrenamiento según la función   a) Hallar k para que sea una función continua. b) Representa la función sabiendo que el periodo de   entrenamiento es de un mes. c) ¿Qué ocurriría con el número de montajes si el entrenamiento   fuera mucho más largo? Solución

jb

Tema 8: Límites. Continuidad

jb
Para empezar el tema: planteamiento didáctico

Programación

Ejercicios con Derive

Criterios de evaluación

Un vistazo global a la unidad: mapa conceptual



Para consultar ejercicios sobre límites, podéis ir a lo publicado años anteriores:

	¤	Tema 8 Límites de funciones. Continuidad.
	¤	Límites (II)
	¤	Límites (III)
	¤	Límites (IV)
	¤	Límites (V)
	¤	Límites (VI)
	¤	Límites (VII)
	¤	Examen Tema 8

Ejercicios sobre Funciones, continuidad y derivabilidad, de la selectividad de la Universidad Illes Balears (desde el año 2001 hasta 2008)

Funciones 1
Funciones 2
Funciones 3
Funciones 4

Los enunciados de los exámenes aquí

Los archivos se abren con Internet Explorer (no funciona con Mozilla) y si sale un aviso:


hay que permitir ejecutar los scripts (Permitir contenido bloqueado...)

También tenéis las soluciones a los ejercicios del libro.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema.
jb

Examen Geometría (Soluciones)

jb

Geometría

1)	Sean u y v dos vectores que forman un ángulo de 45º y que tienen el mismo módulo | u | = | v | = 2. a) ¿Cuál es el módulo de u + v? ¿Y el de u – v? b) Demuestra que u + v y u – v son perpendiculares. Solución
2)	Dados los vectores u = (1, 0, –1), v = (0, 2, –1) y w = (2, –2, 1), se pide: a) El volumen del paralelepípedo determinado por ellos. b) Halla, si existe, el valor de α para que el vector a = (α, α, –6) se pueda expresar como combinación lineal de u y v. Solución
3)	Estudia la posición relativa de las rectas r1 y r2:     Solución
4)	Halla la ecuación del plano que contiene a la recta   y al punto P(2, –3, 1). Solución jb

Examen temas 5 y 6

jb
A petición de los alumnos y para facilitar la superación de la materia de este curso, habrá un examen parcial de geometría.
El examen de los temas 5 y 6 será el
lunes, día 24 a las 19:55
jb

Tema 7: Problemas métricos

jb
Para empezar el tema: planteamiento didáctico

Programación

Ejercicios con Derive

Criterios de evaluación

Un vistazo global a la unidad: mapa conceptual



Para consultar ejercicios sobre vectores, podéis ir a lo publicado años anteriores:

	¤	Problemas métricos
	¤	Problemas métricos (II)
	¤	Problemas métricos (III)
	¤	Tema 7 Ejercicios con Derive
	¤	Problemas métricos (IV)
	¤	Examen Geometría 2008
	¤	Examen Geometría 2010
	¤	Examen 2a Evaluación

También tenéis las soluciones a los ejercicios del libro.

En Matemáticas 2º Bachillerato tenéis más recursos sobre este tema..
jb